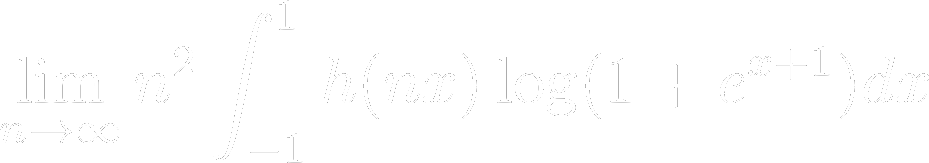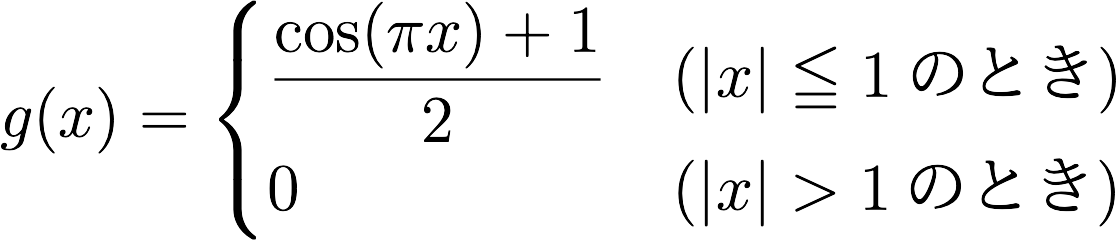2015年度東京大学(理系)第6問
𝒏を正の整数とする。以下の問いに答えよ。
-
関数
𝒈(𝒙)を次のように定める。
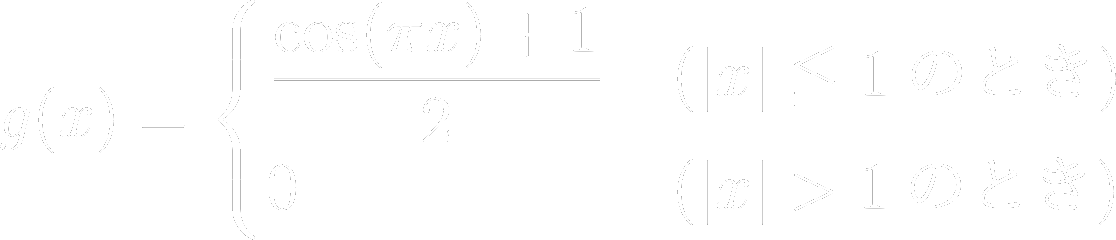
𝒇(𝐱)を連続な関数とし、𝒑、𝒒を実数とする。
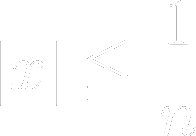
をみたす𝒙に対して𝒑≦𝒇(𝒙)≦𝒒が成り立つとき、次の不等式を示せ。

-
関数
𝒉(𝒙)を次のように定める。
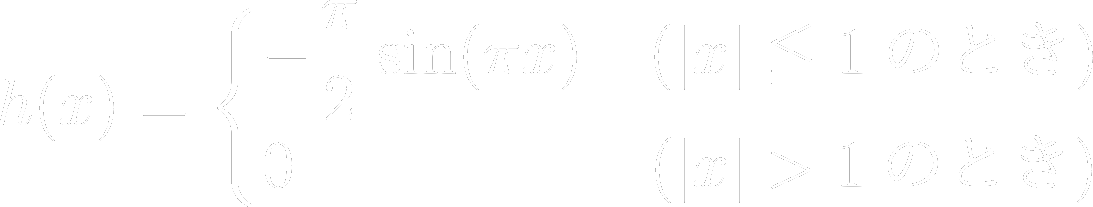
このとき、次の極限を求めよ。